二重振り子の質点軌道を描く
二重振り子の運動方程式
二重振り子とは、下の画像のように、振り子の先にさらに振り子がくっついたような系のことです。
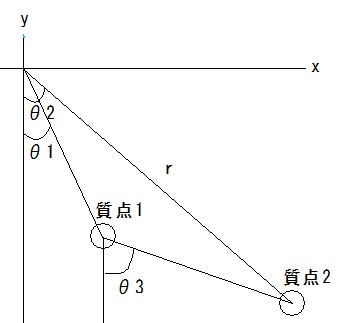
支点から棒でつながれた質点1があり、その質点1の先に棒で質点2をつないでいます。
この振り子について運動方程式を立て、質点2の位置の軌跡をプロットしてみましょう。
簡単にこの系の運動方程式について説明しますが、内容的には大学1~2年相当の力学を習った方向けになります。
そうでない方は読み飛ばしてください。
各質点をつなぐ棒は伸び縮みしないものとすると、この系の自由度は2となります。
即ち、図の中の\(\theta_1\),\(\theta_2\),\(\theta_3\)の内、どれか2つが分かれば、2つの質点の位置を規定できることになります。
ここでは\(\theta_1\),\(\theta_2\)について運動方程式を立てて解くことにしましょう。
棒の長さや質点の質量は、軌跡の形を大きく変える要素ではないため、式を簡単にするために1としておきます。
さて、運動方程式を立てると下の2式になります。
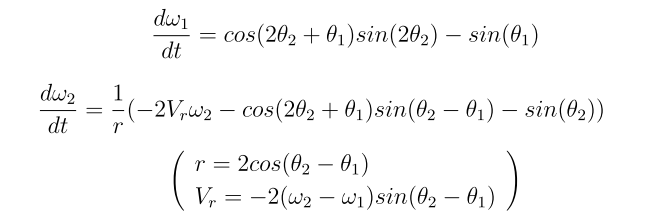
大学で極座標の運動方程式を習った学生の方は、良い練習になるので、上の運動方程式を自力で立ててみてください。
\(\omega_1\),\(\omega_2\)はそれぞれ\(\theta_1\),\(\theta_2\)の角速度を表しています。
この運動方程式を解くと角度と時間の関係が分かりますが、解析的に解くことは無理そうな形をしているため、パソコンで数値計算をします。
octaveという言語のlsodeという解法プログラムを使って求めます。
出てきた角度のデータを各質点の位置に直し、質点2の運動の軌跡をプロットします。
これからいくつかの初期条件でプロットした図を載せていきます。
初期条件の表記は、\((\theta_1 , \omega_1 , \theta_3 , \omega_3)\)の順に書きます。
例えば、\((0.1 , -0.5 , -0.2 , 0.3)\)という表記であれば、
$$\theta_1=0.1$$
$$\omega_1=-0.5$$
$$\theta_3=-0.2$$
$$\omega_3=0.3$$
ということになります。
なお、運動方程式には\(\theta_2\)を使いましたが、初期条件では\(\theta_3\)を使っています。
これは、その方がプログラムが簡単になるからです。
二重振り子の描く軌跡
色々な初期条件で質点2の位置の軌跡をプロットします。
\((0 , 0 , 0 , 0.1)\)
\((0 , 0 , 0 , 0.6)\)
\((0 , 0 , 0 , 0.8)\)
\((0 , 0 , 0.6 , 0)\)
このように、二重振り子の質点は、少し初期条件を変えただけで非常に多様な振る舞いを見せます。
私はこれまで様々な初期条件で二重振り子の軌跡を描いてきました。
これから何回かに渡り、二重振り子の描く軌跡をお見せしていきます。