極座標で花を描く~polar coordinates flowers~
このページでは、高校や大学で習う極座標を使って花や花火のような模様を描いていきます。
内容を理解するには高校で習うsin,cosなどの知識が必要ですが、知っていなくても、ページ後方の画像を見て楽しんでいただければと思います。
学校教育で始めて習う座標といえば、(x,y)を使用した直交座標系です。
平面上のある一点を原点からの縦と横の距離(x,y)を使って表す、分かりやすい座標系です。
それに対し、極座標系とは、下の画像のように原点からの距離rと、x軸からの動径θで平面上の点を表す座標系です。
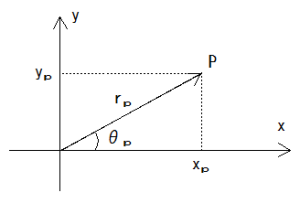
(x,y)と(r,θ)の間には、
$$(x,y) = (r cosθ,r sinθ)$$
という関係が成り立ちます。
この座標系を利用して模様を描いてみましょう。
以下のような式を考えてみます。
$$r = cosθ$$
この式はrとθの関係式になっており、右辺のθの値を決めると、左辺のrの値も決まります。
例えば\(θ = \frac{π}{4}\)とすると、
$$r = cos\frac{π}{4}$$
$$ = \frac{\sqrt{2}}{2}$$
となります。
つまり、x軸から見て\(θ = \frac{π}{4}\)の角度の場所では、原点からの距離が\(\frac{\sqrt{2}}{2}\)ということを意味します。
そこで、座標平面上のx軸から数えて\(θ = \frac{π}{4}\)の角度のところの、原点から\(r=\frac{\sqrt{2}}{2}\)の距離の位置に点を打ちます。
このようにして一周するまで点を打っていくと、下の画像のような模様になります。
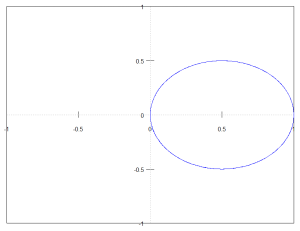
cosθを利用したので、\(θ = 0\) のところでは\(r = 1\)、\(θ = \frac{π}{2}\) のところでは\(r = 0\)となっています。
では、この極座標を利用していくつか模様を描いてみましょう。
画像の下にはその画像を描くために使った式を載せておきます。
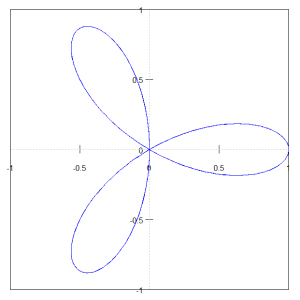
$$r = cos(3θ)$$
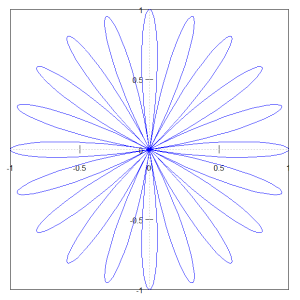
$$r = cos(10θ)$$
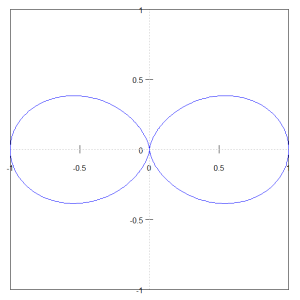
$$r = cos^2(θ)$$
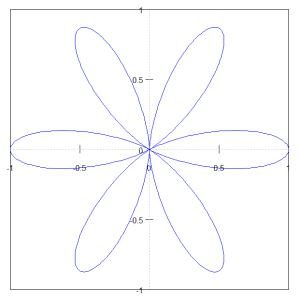
$$r = cos^2(3θ)$$
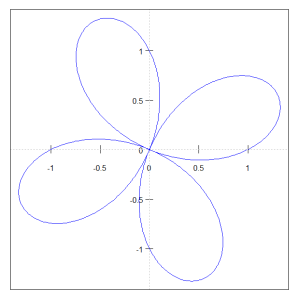
$$r = sin(2θ) + cos(2θ)$$
こうして描いてみると、式と模様の関係性がいくつか見えてきます。