Stephen Wolfram(スティーブン・ウルフラム)の一次元セルオートマトンとrule(ルール)
スティーブン・ウルフラム(Stephen Wolfram)という研究者が研究していたものの中に、セルオートマトンというものがあります。
セルオートマトンというのは計算モデルの一つです。
将棋のようなマス目を用意し、自分のマス目の値を、周囲のマス目の値によって変えていくような計算を行い、シミュレーションなどを行います。

例えば、セルオートマトンを用いた、簡単な温度変化のシミュレーション方法を考えてみましょう。
下の画像のマス目について、温度が高いマスを赤、低いマスを白で塗っています。

シミュレーションのルールとして、注目しているマスの周囲のマス(縦横斜めのマス)について、
・周囲のマスに赤いマスが多い場合は、真ん中のマスを赤くする
・周囲のマスに白いマスが多い場合は、真ん中のマスを白くする
ということを考えます。
上の画像では、真ん中のセルの周り(縦横斜め)に赤いセルが5つ・白いセルが3つあります。
赤の方が多いので、真ん中のマスも赤に変えます。
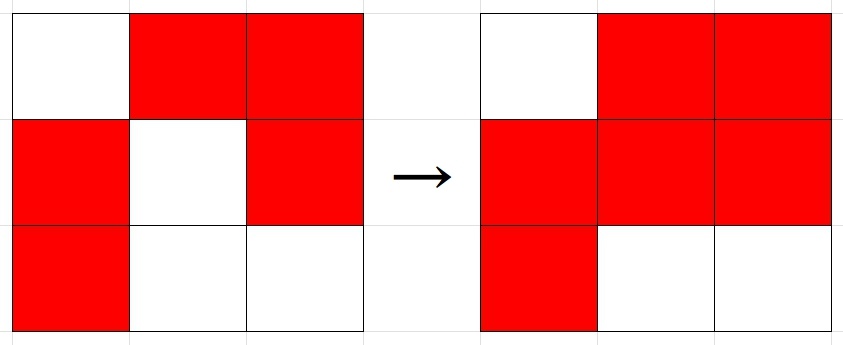
こうして熱がどのように伝わっていくかのモデルを作ることができます。
実際にシミュレーションする場合は、もっとマス目を多くし、ルールも複雑にして計算することになります。
さて、ウルフラムの一次元セルオートマトンというのは以下のようなものです。
まず、白いマス目を横一列に並べ、中心のマスだけ黒く塗っておきます。

そこから、次の8つのルールに従って、下の段に色を塗っていきます。

1.黒いマスが3つ並んでいる場合は、その真ん中のマスの、下のマスを白く塗る(上図の一番左)。
2.同様に、黒・黒・白の場合は黒
3.黒・白・黒の場合は白
4. 黒・白・白の場合は黒
5. 白・黒・黒の場合は白
6. 白・黒・白の場合は白
7. 白・白・黒の場合は白
8. 全て白の場合は白
このようにして、次々と下の段のマスを塗っていくと、下の画像のようになります。
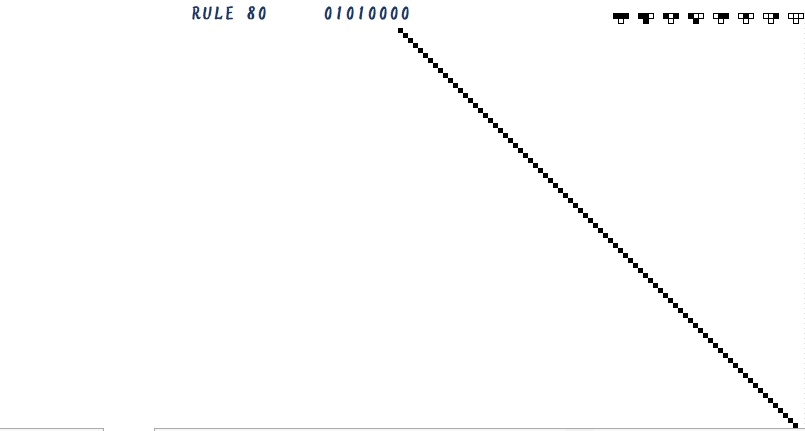
画像の左上にrule80と書いてありますが、80を2進数にすると「01010000」となります。
上述のルールでは、3つのタイルの下のタイルの色が、左から「白黒白黒白白白白」となっていました。

2進数の0に白を、1に黒を対応させ、どのルールを使用しているのかを表しています。
8桁の2進数では10進数の256まで表せるため、ルールは全部で0~255までの256通りあります。
他のルールも見てみましょう。
ルール5は下の画像のようになります。

ルール80とは全く違った図になりました。
さらに、初期条件を変更して描くと、また違った図ができます。
これまでの図では、最初の横一列のセルの中で、真ん中のブロックだけ黒く塗っていました。
今度は最初の横一列のセルを、黒と白ランダムに配置してみましょう。
そしてルール80に従って下段にセルを追加していくと、下の画像のようになります。

ルール5の場合も見てみましょう。

先ほどとは全く違った趣の図になりました。
ちなみに、左端と右端のセルには周期境界条件というものを使っています。

左端のセルで計算を行う際、左側にはもうセルがないため、そのままだとルールが適用できません。
そこで、一番右端のセルを左側のセルとしてルールを適用しています。
右端のセルの計算も同様で、もう右にはセルがないため、左端のセルを利用して色分けを行います。