マンデルブロ集合の図を理解するための基礎知識・虚数と複素数について
前置き
これまでにお見せしたとおり、マンデルブロ集合の式
\(Z_{n+1}=Z_n+C\)
からは驚くほど複雑な図形が生まれてきます。
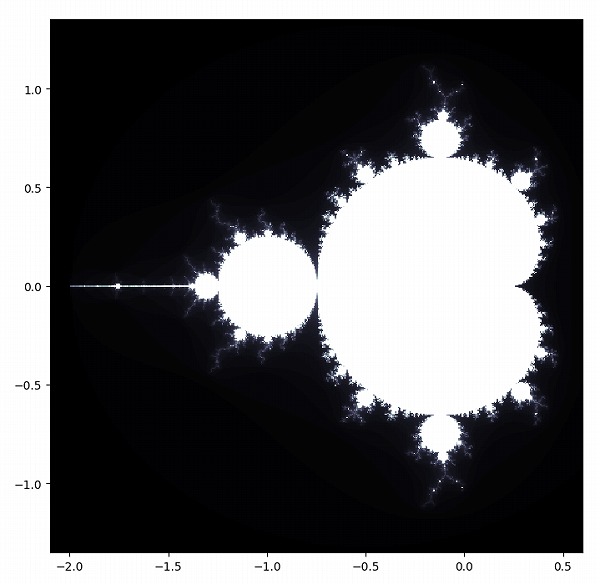
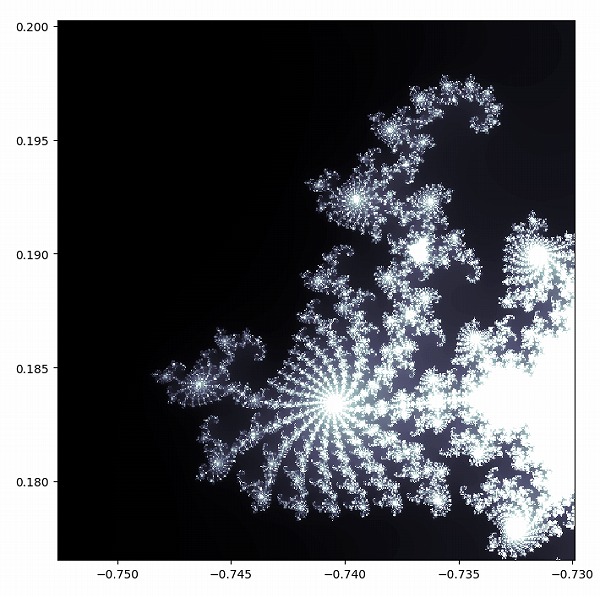

上の式と図形がどう関わっているのか、なぜこのように複雑な図形が描けるのかなどを、数ページに渡り説明していきます。
このページでは、前提知識として必要な虚数と複素数について説明します。
高校の数Ⅱ~数Ⅲの内容に踏み込みますが、中学3年生ぐらいから理解できるような内容となっています。
主に使うのは、中学3年生の展開の計算や、平方根、二次方程式などの知識です。
虚数について
さて、次の方程式を考えてみましょう。
\( x^2=-1\)
この方程式の解についてしばらく考えてみると、これを満たすxは存在しないことが分かります。
上の式を文章で表すと、2乗してマイナス1になる数は何か、という問いになります。
\( 2^2=4\)
\( (-1)^2=1\)
\( (-\frac{1}{4})^2 = \frac{1}{16}\)
思いつくまま適当に計算してみましたが、少し考えてみても、2乗してマイナスになる数は思いつきません。
今までに知っている 整数や分数小数、負の数、無理数(まとめて実数と呼ぶのでした)の中には、2乗してマイナスになる数はなさそうです。
仕方ないので、新しく2乗するとマイナスになる数を作ることにしましょう。
この数を虚数(虚数単位)と名づけ、アルファベットのiを使って表します。
この虚数iについて、
\( i^2=-1\)
が成り立ちます。
虚数単位
虚数単位というのは、この数iが新しい数の基準になっているという意味です。
これまでの数では、1の2倍大きい数は2でした(当たり前の話ですね)。
これまでの数では1が基準になっています。
虚数では、虚数単位iより2倍大きい数は2i、3倍大きい数は3iなどと表します。
虚数の計算
この虚数iは文字と同じように扱うことができ、
\( i+i=2i\)
\( 5i+3i=8i\)
\( -10i+2i=-8i\)
などと計算することができます。
ただ、かけ算のときは文字と違い、\(i^2=-1\)を使って計算しなければいけません
例えば2iを2乗すると、
\( (2i)^2=-4\)
となります。
割り算は文字と同じく、
\( 3i/4i=\frac{3}{4}\)
などと計算できます。
虚数iを基準として、新しい数を表すことができるようになりました。
これで、数の世界が今までよりも広がったことになります。
複素数について
この虚数を使い、さらに新しい数を考えてみましょう。
実数と虚数を組み合わせ、
\( x+iy\)
という数を考えてみます。
この数を複素数と呼びます。
x,yには、5,-2.1,\(\frac{6}{11}\),\(\sqrt{7}\)などの実数が入ります。
複素数は実数xと複素数iy(iかけるy)を足した形になっています。
実数の部分xを実部、虚数の部分iyを虚部と呼びます。
次のページでは、この複素数の四則演算を考えてみましょう。