パソコンの計算速度テスト~マンデルブロ集合の描画時間を計測~
パソコンの計算速度テスト~マンデルブロ集合の描画時間を計測~
計算速度テスト
これまでパソコンのメモリを増設したり、HDDをSSDに換装したりしてパソコンの高速化を行いました。
高速化の結果、パソコンの使い勝手はとても大きく向上したのですが、
どのくらい性能が上がったのか定量的に計測したいと思い、
マンデルブロ集合を描画するのに掛かる時間を計測してみることにしました。
pythonで作成したマンデルブロ集合を描画するプログラムを、
①HDD+メモリ4GB(初期の状態)
②HDD+メモリ8GB
③SSD+メモリ4GB
④SSD+メモリ8GB
の4つの場合で動かし、時間計測を行いました。
マンデルブロ集合とは
マンデルブロ集合というのは、高校の数Ⅲで習う複素数平面上の集合です。
マンデルブロ集合の式を複素数平面上の各点で計算し、
値が収束したらその点は赤、発散するようならば他の色で点を打っていくと、下のような画像を描くことができます。
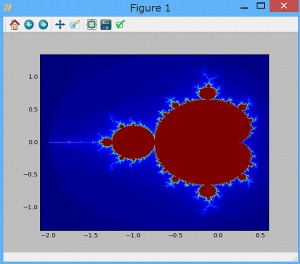
余談ですが、マンデルブロ集合の淵の部分を拡大していくと、何とも不思議な美しい模様が表れます。
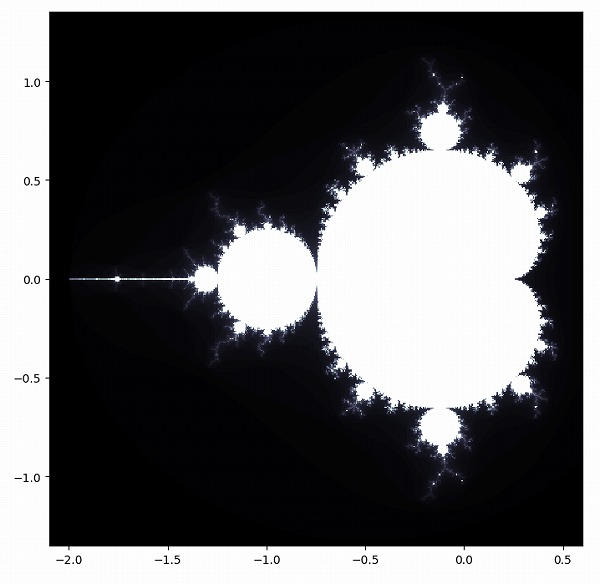
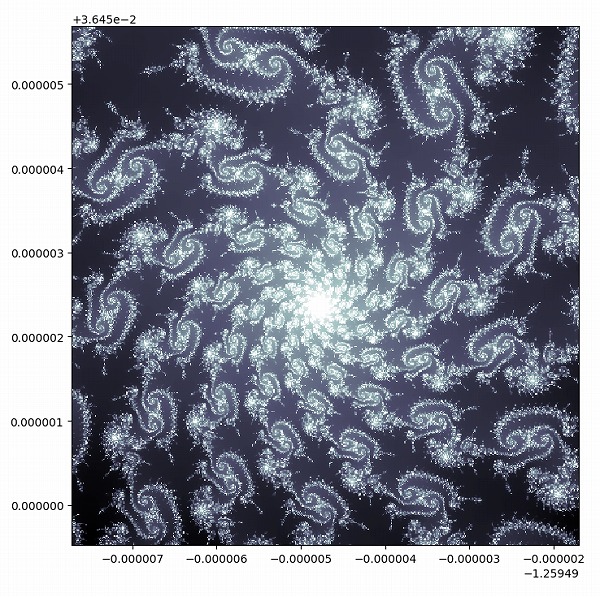
別サイトのルールとパターンでは、マンデルブロ集合やバーニングシップフラクタルなどを拡大した画像を紹介しています。
さて、マンデルブロ集合を描くとき、平面上のたくさんの点で何度も計算を行うため、描くのに時間がかかります。
そのため、パソコンの性能を試すプログラムとして使われることがあります。
今回利用するプログラムはpythonで書いた以下のプログラムです。
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
# -*- coding: utf-8 -*-
#マンデルブロ集合速度テスト
from time import *
import tkinter as tk
import numpy as np
import scipy as sp
import sys
import matplotlib.pyplot as plt
import pylab as pyl
from matplotlib.cm import *
t1=time()
point=[-0.75,0]
length=2.7
thresh=2
roop=100
cut=0.001*length
remin=point[0]-length*0.5
remax=point[0]+length*0.5
immin=-point[1]-length*0.5
immax=-point[1]+length*0.5
aximmin=point[1]-length*0.5
aximmax=point[1]+length*0.5
re=np.arange(remin,remax,cut)
im=np.arange(immin,immax,cut)
M=len(re)
N=len(im)
F=np.zeros((N,M))
d=1j
for m in range(M):
for n in range(N):
z=0+0*d
c=re[m]+im[n]*d
F[n,m]=roop
for k in range(roop):
z=z**2+c
if abs(z)>thresh:
F[n,m]=k
break
t2=time()
print(t2-t1)
plt.imshow(F,extent=[remin,remax,aximmin,aximmax])
plt.axis(“tight")
t3=time()
print(t3-t1)
plt.show()
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
テスト結果と考察
上のプログラムを動かすと、
プログラムを開始してから計算が終了するまでと、プログラム開始から計算と描画が終了するまでの2つの時間を計測し、下の画像のように表示します。
今回は描画までにかかった時間(下の数字)を2回ずつ測り、性能を比較しました。
その2回ずつ測定した結果をそのまま載せます。
結果は・・・
①HDD+メモリ4GB(初期状態)
47.5921秒
48.5961秒
(小数点第5位以下切り捨て)
②HDD+メモリ8GB
44.4821秒
45.0487秒
③SSD+メモリ4GB
43.3910秒
43.2192秒
④SSD+メモリ8GB
42.9536秒
45.4848秒
となりました。
正直、あまり変わっていない気がします・・・
この結果の解釈をしてみましょう。
まず、メモリの交換で速度があまり変わらなかったことについてですが、
メモリの増設・交換のページで、メモリは作業スペースのようなものと書きました。
元々、4GBのメモリでマンデルブロ集合を描いたとき、
作業スペース(メモリの容量)を十分に使えていなかったのではないでしょうか。
なので、メモリを8GBに変えたとしても、使う作業スペースの広さは4GBのときと変わらなかったので、
作業効率が変わらず、時間もそれほど変わらなかったのだと思います。
次に、HDDをSSDに変えてもそれほど速度が変わらなかったことについてですが、
HDDをSSDに変えると、ドライブに入っているファイルにアクセスする速度が速くなります。
ところが、マンデルブロ集合を描くときは、何度もドライブにアクセスする必要がなかったため、
ファイル読み込みが高速化されても、計算速度に大して影響がなかったのではないでしょうか。
マンデルブロ集合の描画では、メモリの交換やSSDへの換装の効果が分からなかったので、
次回は別のテストを行ってみようと思います。