マンデルブロ集合をpythonで描くプログラムのコード
pythonでマンデルブロ集合を描く
pythonでマンデルブロ集合を描くための、ベーシックなプログラムを紹介します。
別のページでは、バーニングシップフラクタルを描画するプログラムも紹介しています。
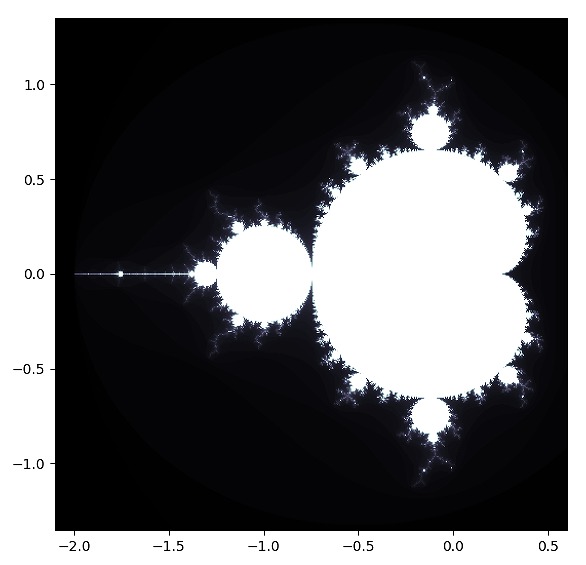
プログラム中ではnumpyとmatplotlibを使っているため、両者のインストールが必要です。
pythonは動的な言語のため、C言語などと違い、マンデルブロ集合を描くのに結構時間がかかります。
pythonを用いて高速に描くには、計算方法に手を加えるか、cythonを使うなどの工夫が必要です。
下記のコードを拡張子.pyのファイルにコピペし、import コマンドで読み込めばマンデルブロ集合が描けるはずです。
マンデルブロ集合を描くプログラム
↓以下プログラムです
import numpy as np
import matplotlib.pyplot as plt
point=[-0.75,0]
length=2.7
thresh=2
roop=100
cut=0.001*length
remin=point[0]-length*0.5
remax=point[0]+length*0.5
immin=-point[1]-length*0.5
immax=-point[1]+length*0.5
aximmin=point[1]-length*0.5
aximmax=point[1]+length*0.5
re=np.arange(remin,remax,cut)
im=np.arange(immin,immax,cut)
M=len(re)
N=len(im)
F=np.zeros((N,M))
d=1j
for m in range(M):
for n in range(N):
z=0+0*d
c=re[m]+im[n]*d
F[n,m]=roop
for k in range(roop):
z=z**2+c
if abs(z)>thresh:
F[n,m]=k
break
plt.imshow(F,extent=[remin,remax,aximmin,aximmax],cmap=plt.get_cmap("bone"))
plt.axis("tight")
plt.show()
簡単なコードの説明
コードを簡単に説明します。
まず、描画範囲を縦横0.001の長さで正方形のセルに区切ります。
各セルについてマンデルブロ集合の式
z=z**2+c
を計算し、zの絶対値が2(thresh)を超えないか確認していきます。
2を超えるかどうか、また、超えた場合は何回の計算で超えたのかを、各セルに値として代入していきます。
「point」という変数は、描画する座標の中心を表しています。
「length」は描画する範囲の縦と横の長さを表します。
lengthを小さくすると、マンデルブロ集合を拡大して表示させることができます。
lengthを小さくしながらpointを描きたい部分に合わせることで、マンデルブロ集合の淵を拡大して見ることができます。
「roop」というのは各セルに対しての計算回数です。
上のプログラムではroop=100に設定しているため、100回計算して計算値が2を超えなければ、そこでの値は収束すると判定します。
マンデルブロ集合の淵に近づくほど、計算値が2を超えるかどうかを判別するのにより多くの計算回数が必要になります。
淵を拡大する場合は、roopを多くしていく必要があります。
ただ、その分プログラム終了までにかかる時間が多くなります。
z=z**2+c
というのがマンデルブロ集合の式です。
これを、
z=(abs(z.real)+abs(z.imag)*1j)**2+cとすればバーニングシップフラクタルを描くことができます。