エノン・ハイレス(henon-heiles)ポテンシャルのポアンカレ断面図
エノンハイレスポテンシャルとは、
$$U(x,y)=\frac{1}{2}k(x^2+y^2)+x^2y-\frac{1}{3}y^3$$
で表されるポテンシャルのことです。
図にすると下の画像のようになります。
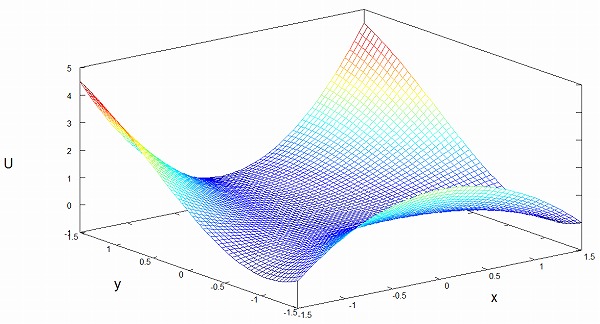
ポテンシャルとは、高校物理で習う位置エネルギーのことです。
簡単に例えると、床や地面のような物です。
床と同じで上に物を置くと、低い方へと物体が動きます。
このエノン・ハイレスポテンシャルの中心には、下の画像のようにおにぎり形のくぼみがあります。
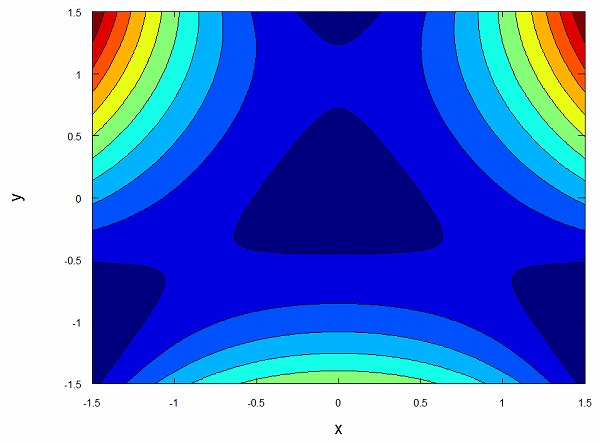
中心\((x,y)=(0,0)\)に質点を置き、一方向に動かしてみると、下の画像のように質点が運動します。
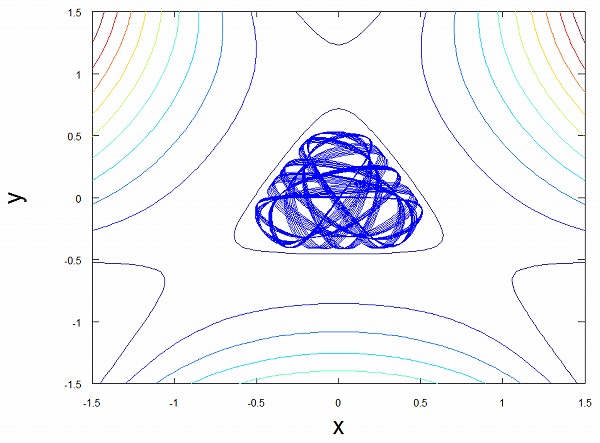
さて、上の図の真ん中に縦線(直線x=0)を引きます。
質点がその線を通る時の、yの値とy方向の速度を計算します。
そうしてy座標の値と速度のy成分を点でプロットしていくと、下図のようになります。
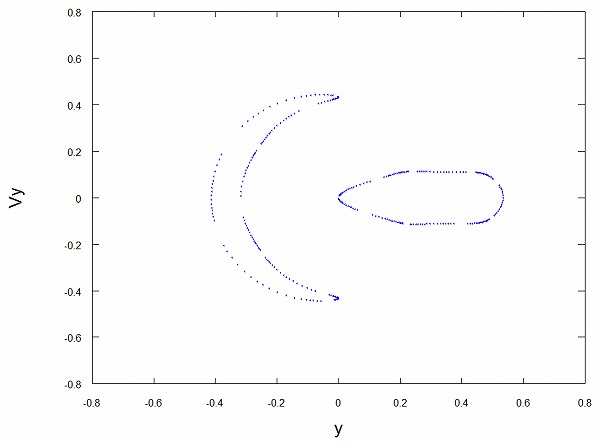
何やら特徴的な形が現れました。
同じように、\( (x,y)=(0,0)\) から質点を色々な方向に運動させ、x=0を通る時のy座標と速度のy成分をプロットしていくと、下図のような結果になります。
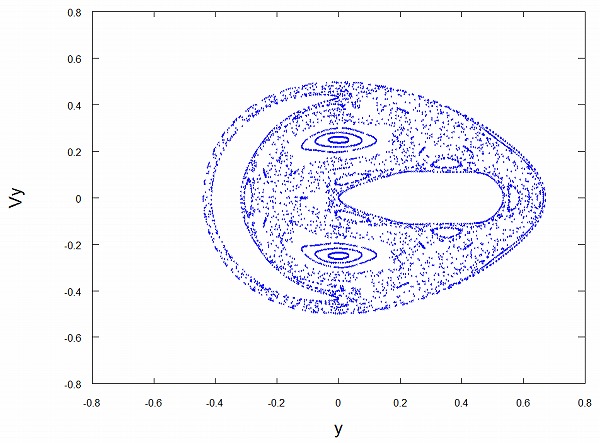
有名な笑う顔のようなパターンが現れました。
今後別のページで、ポアンカレ断面とは何かということや、具体的な描き方について書いていきたいと思います。