シェルピンスキーガスケットとバーンスレーのシダ~Sierpinski gasket & Barnsley fern~
このページの参考文献:小柳義夫「計算物理学 基礎編・応用編」・朝倉書店
漸化式を利用して面白い物を描いてみましょう。
ちなみに漸化式というのは、
\(x_{n+1}=x_n+3\)
といったように、数列の項間の関係を表す式です。
例えば\(x_1=4\)として上の式に代入していくと、
\(x_2=x_1+3\)
\(x_2=4+3\)
\(=7\)
\(x_3=7+3\)
\(=10\)
といったように各項が定まっていきます。
さて、今回使うのは下のような式です。
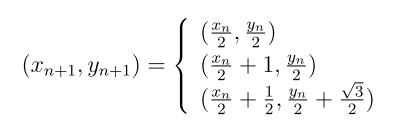
先ほどはxのみでしたが、この式ではxとyの2つの文字が使われています。
括弧の中にカンマで区切られた式が入っていますが、カンマの左がxについての式、右側がyについての式となっています。
また、式が3本(全部で6本)になっているのも先ほどの式と違います。
どの式を使うのかは確率によって決めます。
ではこの式を使って絵を描いてみましょう。
初期条件を\((x_1=1,y_1=0)\)とし、グラフ上の(1,0)に点を打ちます。
次に、どの式を使うのかを決めます。
さいころを振り、1か2が出たら一番目の式、3か4が出たら二番目の式、5か6が出たら三番目の式を使います。
(それぞれ\(\frac{1}{3}\)の確率で式を決めるということですが、実際にプログラミングで描くときには乱数というものを使って式を決めます)
例えばさいころで1の目が出たとしてみましょう。
その場合は一番上の式を使うわけですが、
\((x_2,y_2)=(\frac{x_1}{2},\frac{y_2}{2})\)
\(=(\frac{1}{2},0)\)
となり、次の点\((x_2,y_2)=(\frac{1}{2},0)\)が決まったので、そこに点を打ちます。
同じ様にまたさいころを振って次の式を決め、計算をして点を打ち、さらにさいころを振っていきます。
このような作業を30000回繰り返すと、下の画像のような図形を描くことができます。
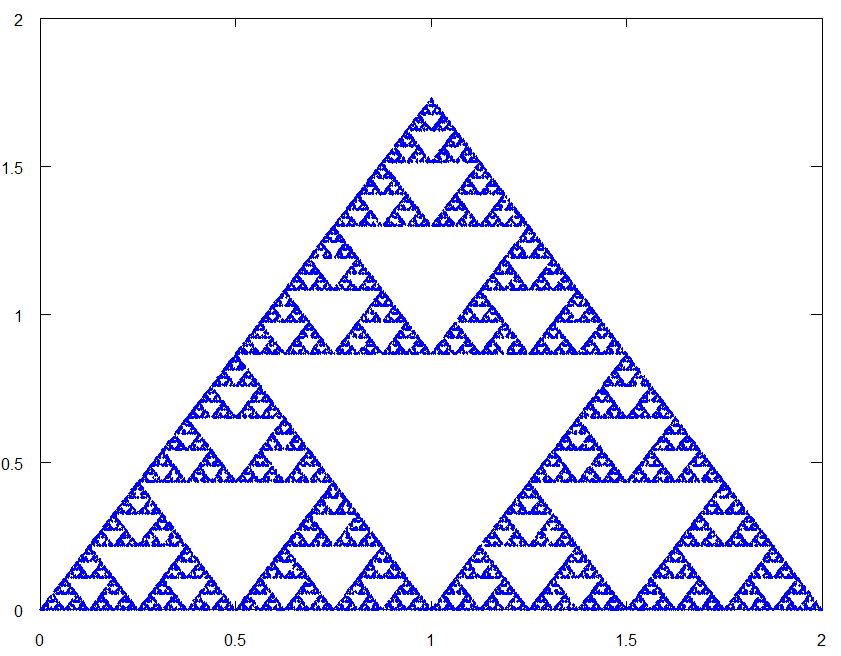
これはシェルピンスキーガスケットという名前の図形です。
さて、先ほどの式を変えて模様を描いてみましょう。
使うのは下の式です。

今度はそれぞれの式を等確率に使うのではなく、式の右に付いている確率をもとにどの式を使うのかを決めます。
先ほどと同じ様に30000回計算と打点を繰り返すと、下の画像のような模様が描けます。
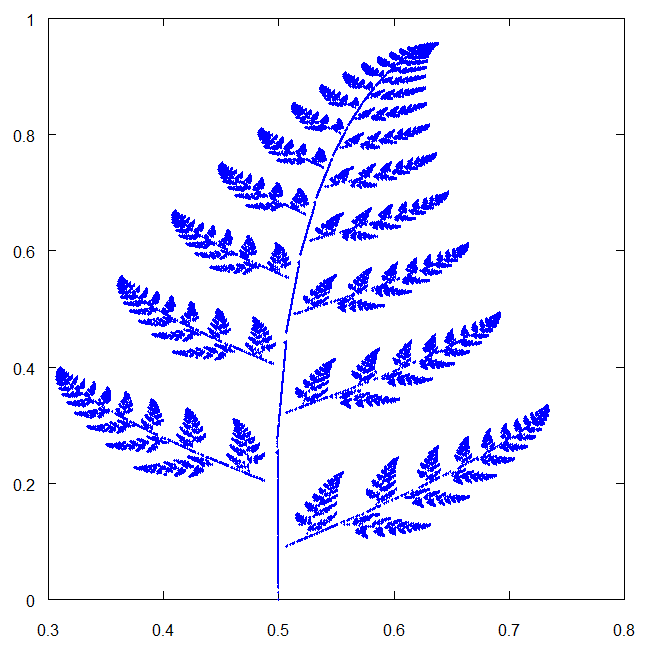
これはシダ植物のように見えますが、バーンスレーのシダと呼ばれているそうです。
計算式から植物のような模様を描けるというのは、実に不思議なことだと思いませんか。
なぜ式で植物が描けるのかということについて意見を書いてみます。
植物を観察していると、一本の茎から枝が何本も伸び、その枝からもさらに枝が伸びている、いわゆる自己相似の形をしていることが多いように思います。
上のバーンスレーのシダも自己相似のような形をしています。
このような特徴は葉脈にも見られます。
何かを作る時、最小単位の構造を一個の型として作っておき、それを組み合わせて全体を作れば、最小限の情報量で簡単に体を作ることができます。
その型となる物が数式なのではないでしょうか。
上のような数式が植物のDNAかどこかに保存されており、それを基にして体を形作っているから、植物は自己相似のような形をしていることが多いのではないでしょうか。
生物に関しては素人なので、以上に述べたことは完全な憶測にすぎません。
いずれ実験か何かで実証できたらと思います。
なお、冒頭で紹介した参考文献では、他にも木を描く式などが載っています。
物理現象をプログラミングで解析する方法がたくさん載っており、計算物理学をするうえで非常におすすめの本です。